Дерево решений CART (Classification and Regressoin Tree) — алгоритм классификации и регрессии, основанный на бинарном дереве и являющийся фундаментальным компонентом случайного леса и бустингов, которые входят в число самых мощных алгоритмов машинного обучения на сегодняшний день. Деревья также могут быть не бинарными в зависимости от реализации. К другим популярным реализациям решающего дерева относятся следующие: ID3, C4.5, C5.0.
Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).
Структура дерева решений
Решающее дерево состоит из следующих компонентов: корневой узел, ветви (левая и правая), решающие и листовые (терминальные) узлы. Корневой и решающие узлы представляют из себя вопросы с пороговым значением для разделения тренировочного набора на части (левая и правая), а листья являются конечными прогнозами: среднее значений в листе для регрессии и статистическая мода для классификации.
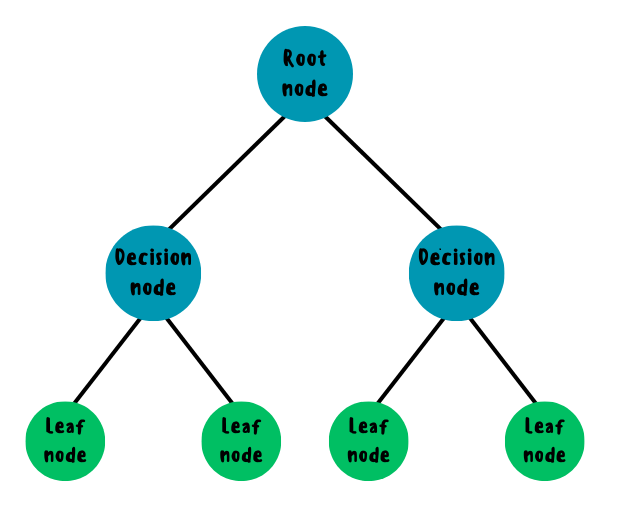
Структура CART
Каждый листовой узел соответствует определённой прямоугольной области на графике границ решений между двумя признаками. Если на графике соседние участки имеют одинаковое значение, то они автоматически объединяются и представляются как одна большая область.
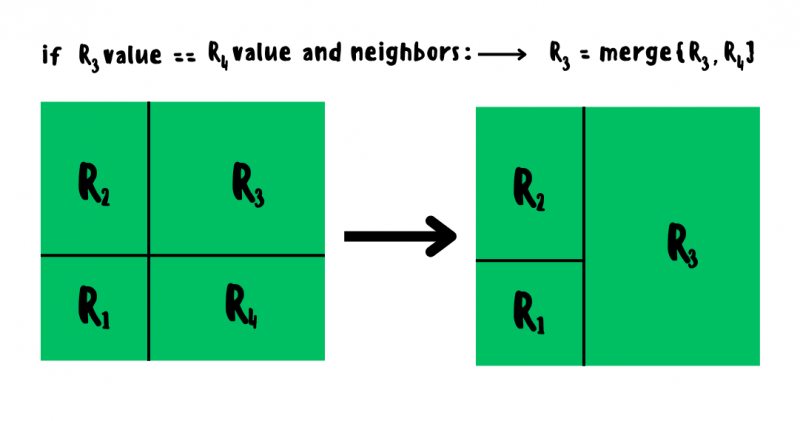
График границ решений
Выбор наилучшего разбиения
Выбор наилучшего разбиения при построении решающего узла в дереве напоминает игру, в которой нужно угадать знаменитость, задавая вопросы, на которые можно лишь услышать ответ “да” либо “нет”. Логично, что для быстрого поиска правильного ответа необходимо задавать вопросы, которые исключат наибольшее количество неверных вариантов, например, вопрос про “пол” позволит исключить сразу же половину вариантов, в то время как вопрос про “возраст” будет менее информативным. Проще говоря, выбор наилучшего вопроса заключается в поиске признака, определённое значение которого лучше всего отделяет правильный ответ от неправильных.
Показатель того, насколько хорошо вопрос в решающем узле позволяет отделить верный ответ от неверных, называется мерой загрязнённости узла. В случае классификации для оценки качества разбиения узла используются следующие критерии:
-
Неопределённость (загрязнённость) Джини — мера разнообразия в распределении вероятностей классов. Если все элементы в узле принадлежат к одному классу, то неопределённость Джини равна 0, а в случае равномерного распределения классов в узле неопределённость Джини равна 0.5.

-
Энтропия Шеннона — мера неопределённости или беспорядка классов в узле. Она характеризует количество информации, которое необходимо для описания состояния системы: чем выше значение энтропии, тем менее упорядочена система и наоборот.

-
Ошибка классификации — величина, отображающая долю неправильно классифицированных элементов в узле: чем меньше данное значение, тем меньше загрязнённость в узле.

В данном случае

— это доля k-го класса среди обучающих образцов в i-ом узле.
На практике чаще всего используются неопределённость Джини и энтропия Шеннона за счёт большей информативности. Как видно из графика для случая бинарной классификации (где P+ — вероятность принадлежности к классу “+”), график удвоенной неопределённости Джини очень схож с графиком энтропии Шеннона: в первом случае будут получаться чуть менее сбалансированные деревья, однако при работе с большими датасетами неопределённость Джини более предпочтительна за счёт меньшей вычислительной сложности.
Код для отрисовки графика
import numpy as np import matplotlib.pyplot as plt def gini(probas): return np.array([1- (p ** 2 + (1-p) ** 2) for p in probas]) def entropy(probas): return np.array([-1 * (p * np.log2(p) + (1-p) * np.log2(1-p)) for p in probas]) def misclass_error_rate(probas): return np.array([1 - max([p, 1-p]) for p in probas]) probas = np.linspace(0, 1, 250) plt.plot(probas, entropy(probas), label="Shannon's entropy") plt.plot(probas, 2 * gini(probas), label="Gini impurity x 2") plt.plot(probas, 2 * misclass_error_rate(probas), label="Misclass error x 2") plt.plot(probas, gini(probas), label="Gini impurity") plt.plot(probas, misclass_error_rate(probas), label="Misclass error") plt.title("Splitting criteria from P+ (binary classification case)") plt.xlabel("P+") plt.ylabel("Impurity") plt.legend();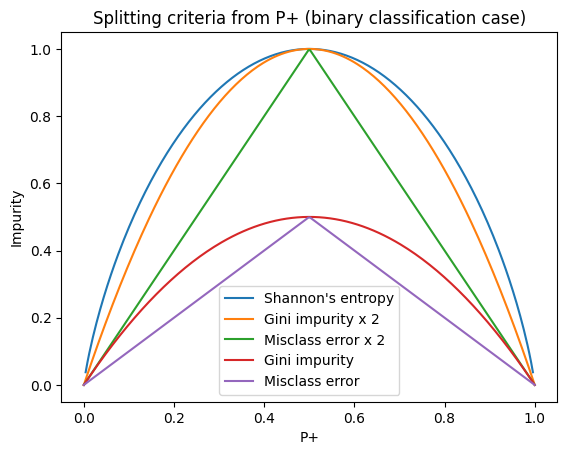
В случае регрессии для оценки качества разбиения узла чаще всего используется среднеквадратичная ошибка, но также могут быть использованы Friedman MSE и MAE.
Функция потерь
Так как же в конечном счёте происходит выбор наилучшего разбиения? После выбора одного из критериев оценки качества разбиения узла (например, неопределённость Джини или MSE), для всех уникальных значений признака берутся их пороговые значения, отсортированные по возрастанию и представленные как среднее арифметическое между соседними значениями. Далее обучающий набор разделяется на 2 поднабора (узла): всё что меньше либо равно текущего порогового значения идёт в левый поднабор, а всё что больше — в правый. Для полученных поднаборов рассчитываются загрязнённости на основе выбранного критерия, после чего их взвешенная сумма представляется как функция потерь, значение которой будет соответствовать пороговому значению признака. Порог с наименьшим значением функции потерь в обучающем наборе (поднаборе) будет наилучшим разбиением.
Функции потерь будут иметь следующий вид:
-
для классификации:

-
для регрессии:

где

.
В случае с энтропией используется немного иной подход: рассчитывается так называемый информационный прирост — разница энтропий родительского и дочерних узлов. Порог с максимальным информационным приростом в обучающем наборе/поднаборе будет соответствовать наилучшему разбиению. :

где

— условие (вопрос) для разбиения поднабора

.
Для наглядности рассмотрим следующий пример. Допустим, у нас есть 4 кота и 4 собаки, а также нам известны их некоторые визуальные признаки: “рост”, “уши” (висячие и заострённые стоячие) и “усы” (наличие либо отсутствие). Как в дереве решений строится корневой узел для классификации собак и котов? Очень просто: сначала для каждого признака животные разделяются на 2 группы согласно вопросу, после чего для каждой из групп рассчитывается неопределённость Джини. Пороговое значение признака с наименьшим значением функции потерь (взвешенной суммой неопределённостей) будет использоваться для разбиения корневого (решающего) узла. В данном случае признак “рост” имеет наименьшую загрязнённость и вопрос в решающем узле будет выглядеть как “рост ⩽ 20 см”.
Стоит добавить, что в случае с категориальными признаками происходит их бинаризация и вопросы выглядят следующим образом: “уши ⩽ 0.5”, “усы ⩽ 0.5”. Когда категориальные признаки могут принимать более 2 значений, применяются другие виды кодирования, например label или one-hot encoding.
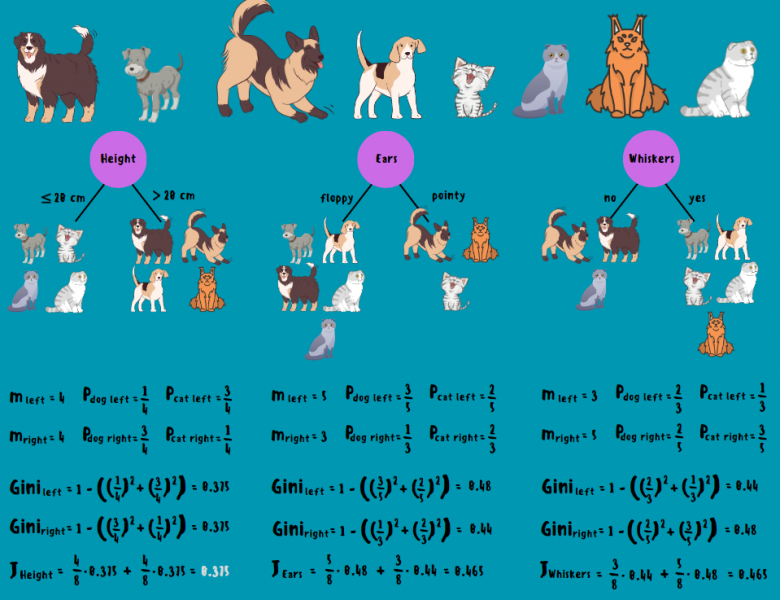
Принцип работы дерева решений (CART)
Алгоритм строится следующим образом:
-
1) создаётся корневой узел на основе наилучшего разбиения;
-
2) тренировочный набор разбивается на 2 поднабора: всё что соответствует условию разбиения отправляется в левый узел, остальное — в правый;
-
3) далее рекурсивно для каждого тренировочного поднабора повторяются шаги 1-2 пока не будет достигнут один из основных критериев останова: максимальная глубина, максимальное количество листьев, минимальное количество наблюдений в листе или минимальное снижение загрязнения в узле.
Регуляризация дерева решений
Выращенная без ограничений древовидная структура в той или иной степени будет склонна к переобучению и для решения данной проблемы используется 2 подхода: pre-pruning (ограничение роста дерева во время построения любым из критериев останова) и post-pruning (отсечение лишних ветвей после полного построения). Второй подход является более деликатным так как позволяет получить несимметричную и более точную древовидную структуру, оставляя лишь самые информативные решающие узлы.
Существует 2 типа post-puning’а:
-
Top-down pruning — метод, при котором проверка и обрезка наименее информативных ветвей начинается с корневого узла. Данный метод обладает относительно низкой вычислительной сложностью, однако, как и в случае с pre-pruning’ом, его главным недостатком также является возможность недообучения за счёт удаления ветвей, которые могли потенциально содержать информативные узлы. К самым известным видам данного прунинга относятся следующие:
-
Pessimistic Error Pruning (PEP), когда обрезаются ветви с наибольшей ожидаемой ошибкой, порог которой устанавливается заранее;
-
Critical Value Pruning (CVP), когда обрезаются ветви, информативность которых меньше определённого критического значения.
-
-
Bottom-up pruning — метод, при котором проверка и обрезка наименее информативных ветвей начинается с листьев. В данном случае получаются более точные деревья за счёт полного обхода снизу-вверх и оценки каждого решающего узла, однако это приводит к увеличению вычислительной сложности. Самыми популярными видами данного прунинга являются следующие:
-
Minimum Error Pruning (MEP), когда происходит поиск дерева с наименьшей ожидаемой ошибкой на отложенной выборке;
-
Reduced Error Pruning (REP), когда решающие узлы удаляются до тех пор, пока не падает точность, измеренная на отложенной выборке;
-
Cost-complexity pruning (CCP), когда строится серия поддеревьев через удаление слабейших узлов в каждом из них с помощью коэффициента, рассчитанного как разность ошибки корневого узла поддерева и общей ошибки его листьев, а выбор наилучшего поддерева производится на тестовом наборе или с помощью k-fold кросс-валидации.
-
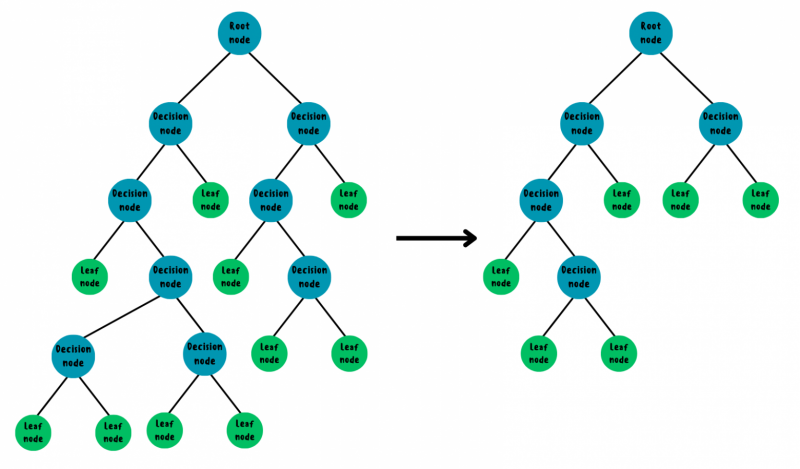
Дерево до и после post-pruning’а
Minimal cost-complexity pruning
В реализации scikit-learn для деревьев решений используется модификация cost-complexity pruning, которая работает следующим образом:
-
1) сначала строится полное дерево без ограничений;
-
2) далее абсолютно для всех узлов в дереве рассчитывается ошибка на основе взвешенной загрязнённости в случае классификации или взвешенной MSE в случае регрессии;
-
3) для каждого поддерева в дереве подсчитывается совокупная ошибка его листьев;
-
4) для каждого поддерева в дереве рассчитывается коэффициент альфа, представленный как разность ошибки корневого узла поддерева и совокупная ошибка его листьев;
-
5) поддерево с наименьшим

удаляется и становится листовым узлом, а сам коэффициент хранится в массиве cost_complety_pruning_path и соответствует новому обрезанному дереву;
-
6) шаги 2-5 рекурсивно повторяются для каждого поддерева до тех пор, пока обрезка не дойдёт до корневого узла.
Если задавать определённое значение

изначально, то данный коэффициент применится к каждому поддереву и в итоге останется поддерево с наименьшей ошибкой среди всех поддеревьев, а выбор наилучшего

из cost_complety_pruning_path для получения самого точного поддерева производится на тестовом наборе или с помощью k-fold кросс-валидации.
Формулы для расчётов
Регуляризация дерева:

Эффективный

:

Ошибка решающего

или листового

узлов для классификации:

Ошибка решающего

или листового

узлов для регрессии:

Совокупная ошибка листьев в дереве/поддереве:

T — число терминальных (листовых) узлов.
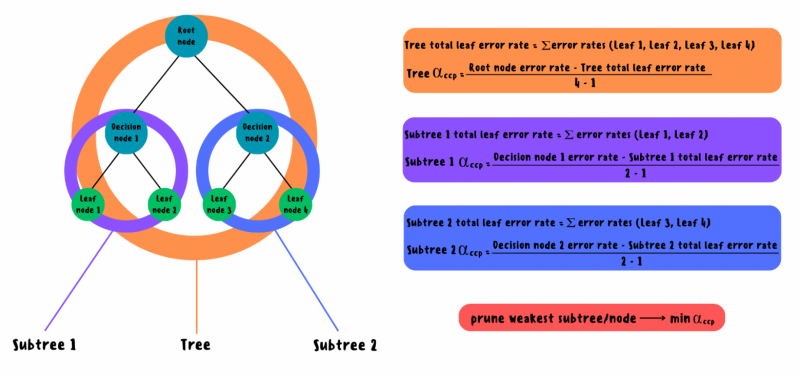
Схема работы cost-complexity pruning’а для простейшего дерева
Импорт необходимых библиотек
import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_linnerud from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, mean_absolute_percentage_error from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor, plot_tree from mlxtend.plotting import plot_decision_regions from copy import deepcopy from pprint import pprintРеализация на Python с нуля
В оригинальном дереве для создания узлов и хранения в них информации используется отдельный класс, но в данном случае дерево и вся информация об узлах хранятся в словаре с ключами в строчном формате. Такое изменение используется для возможности вывода полученного дерева и сравнения с реализацией scikit-learn.
class DecisionTreeCART: def __init__(self, max_depth=100, min_samples=2, ccp_alpha=0.0, regression=False): self.max_depth = max_depth self.min_samples = min_samples self.ccp_alpha = ccp_alpha self.regression = regression self.tree = None self._y_type = None self._num_all_samples = None def _set_df_type(self, X, y, dtype): X = X.astype(dtype) y = y.astype(dtype) if self.regression else y self._y_dtype = y.dtype return X, y @staticmethod def _purity(y): unique_classes = np.unique(y) return unique_classes.size == 1 @staticmethod def _is_leaf_node(node): return not isinstance(node, dict) # if a node/tree is a leaf def _leaf_node(self, y): class_index = 0 return np.mean(y) if self.regression else y.mode()[class_index] def _split_df(self, X, y, feature, threshold): feature_values = X[feature] left_indexes = X[feature_values <= threshold].index right_indexes = X[feature_values > threshold].index sizes = np.array([left_indexes.size, right_indexes.size]) return self._leaf_node(y) if any(sizes == 0) else left_indexes, right_indexes @staticmethod def _gini_impurity(y): _, counts_classes = np.unique(y, return_counts=True) squared_probabilities = np.square(counts_classes / y.size) gini_impurity = 1 - sum(squared_probabilities) return gini_impurity @staticmethod def _mse(y): mse = np.mean((y - y.mean()) ** 2) return mse @staticmethod def _cost_function(left_df, right_df, method): total_df_size = left_df.size + right_df.size p_left_df = left_df.size / total_df_size p_right_df = right_df.size / total_df_size J_left = method(left_df) J_right = method(right_df) J = p_left_df*J_left + p_right_df*J_right return J # weighted Gini impurity or weighted mse (depends on a method) def _node_error_rate(self, y, method): if self._num_all_samples is None: self._num_all_samples = y.size # num samples of all dataframe current_num_samples = y.size return current_num_samples / self._num_all_samples * method(y) def _best_split(self, X, y): features = X.columns min_cost_function = np.inf best_feature, best_threshold = None, None method = self._mse if self.regression else self._gini_impurity for feature in features: unique_feature_values = np.unique(X[feature]) for i in range(1, len(unique_feature_values)): current_value = unique_feature_values[i] previous_value = unique_feature_values[i-1] threshold = (current_value + previous_value) / 2 left_indexes, right_indexes = self._split_df(X, y, feature, threshold) left_labels, right_labels = y.loc[left_indexes], y.loc[right_indexes] current_J = self._cost_function(left_labels, right_labels, method) if current_J <= min_cost_function: min_cost_function = current_J best_feature = feature best_threshold = threshold return best_feature, best_threshold def _stopping_conditions(self, y, depth, n_samples): return self._purity(y), depth == self.max_depth, n_samples < self.min_samples def _grow_tree(self, X, y, depth=0): current_num_samples = y.size X, y = self._set_df_type(X, y, np.float128) method = self._mse if self.regression else self._gini_impurity if any(self._stopping_conditions(y, depth, current_num_samples)): RTi = self._node_error_rate(y, method) # leaf node error rate leaf_node = f'{self._leaf_node(y)} | error_rate {RTi}' return leaf_node Rt = self._node_error_rate(y, method) # decision node error rate best_feature, best_threshold = self._best_split(X, y) decision_node = f'{best_feature} <= {best_threshold} | ' f'as_leaf {self._leaf_node(y)} error_rate {Rt}' left_indexes, right_indexes = self._split_df(X, y, best_feature, best_threshold) left_X, right_X = X.loc[left_indexes], X.loc[right_indexes] left_labels, right_labels = y.loc[left_indexes], y.loc[right_indexes] # recursive part tree = {decision_node: []} left_subtree = self._grow_tree(left_X, left_labels, depth+1) right_subtree = self._grow_tree(right_X, right_labels, depth+1) if left_subtree == right_subtree: tree = left_subtree else: tree[decision_node].extend([left_subtree, right_subtree]) return tree def _tree_error_rate_info(self, tree, error_rates_list): if self._is_leaf_node(tree): *_, leaf_error_rate = tree.split() error_rates_list.append(np.float128(leaf_error_rate)) else: decision_node = next(iter(tree)) left_subtree, right_subtree = tree[decision_node] self._tree_error_rate_info(left_subtree, error_rates_list) self._tree_error_rate_info(right_subtree, error_rates_list) RT = sum(error_rates_list) # total leaf error rate of a tree num_leaf_nodes = len(error_rates_list) return RT, num_leaf_nodes @staticmethod def _ccp_alpha_eff(decision_node_Rt, leaf_nodes_RTt, num_leafs): return (decision_node_Rt - leaf_nodes_RTt) / (num_leafs - 1) def _find_weakest_node(self, tree, weakest_node_info): if self._is_leaf_node(tree): return tree decision_node = next(iter(tree)) left_subtree, right_subtree = tree[decision_node] *_, decision_node_error_rate = decision_node.split() Rt = np.float128(decision_node_error_rate) RTt, num_leaf_nodes = self._tree_error_rate_info(tree, []) ccp_alpha = self._ccp_alpha_eff(Rt, RTt, num_leaf_nodes) decision_node_index, min_ccp_alpha_index = 0, 1 if ccp_alpha <= weakest_node_info[min_ccp_alpha_index]: weakest_node_info[decision_node_index] = decision_node weakest_node_info[min_ccp_alpha_index] = ccp_alpha self._find_weakest_node(left_subtree, weakest_node_info) self._find_weakest_node(right_subtree, weakest_node_info) return weakest_node_info def _prune_tree(self, tree, weakest_node): if self._is_leaf_node(tree): return tree decision_node = next(iter(tree)) left_subtree, right_subtree = tree[decision_node] left_subtree_index, right_subtree_index = 0, 1 _, leaf_node = weakest_node.split('as_leaf ') if weakest_node is decision_node: tree = weakest_node if weakest_node in left_subtree: tree[decision_node][left_subtree_index] = leaf_node if weakest_node in right_subtree: tree[decision_node][right_subtree_index] = leaf_node self._prune_tree(left_subtree, weakest_node) self._prune_tree(right_subtree, weakest_node) return tree def cost_complexity_pruning_path(self, X: pd.DataFrame, y: pd.Series): tree = self._grow_tree(X, y) # grow a full tree tree_error_rate, _ = self._tree_error_rate_info(tree, []) error_rates = [tree_error_rate] ccp_alpha_list = [0.0] while not self._is_leaf_node(tree): initial_node = [None, np.inf] weakest_node, ccp_alpha = self._find_weakest_node(tree, initial_node) tree = self._prune_tree(tree, weakest_node) tree_error_rate, _ = self._tree_error_rate_info(tree, []) error_rates.append(tree_error_rate) ccp_alpha_list.append(ccp_alpha) return np.array(ccp_alpha_list), np.array(error_rates) def _ccp_tree_error_rate(self, tree_error_rate, num_leaf_nodes): return tree_error_rate + self.ccp_alpha*num_leaf_nodes # regularization def _optimal_tree(self, X, y): tree = self._grow_tree(X, y) # grow a full tree min_RT_alpha, final_tree = np.inf, None while not self._is_leaf_node(tree): RT, num_leaf_nodes = self._tree_error_rate_info(tree, []) current_RT_alpha = self._ccp_tree_error_rate(RT, num_leaf_nodes) if current_RT_alpha <= min_RT_alpha: min_RT_alpha = current_RT_alpha final_tree = deepcopy(tree) initial_node = [None, np.inf] weakest_node, _ = self._find_weakest_node(tree, initial_node) tree = self._prune_tree(tree, weakest_node) return final_tree def fit(self, X: pd.DataFrame, y: pd.Series): self.tree = self._optimal_tree(X, y) def _traverse_tree(self, sample, tree): if self._is_leaf_node(tree): leaf, *_ = tree.split() return leaf decision_node = next(iter(tree)) # dict key left_node, right_node = tree[decision_node] feature, other = decision_node.split(' <=') threshold, *_ = other.split() feature_value = sample[feature] if np.float128(feature_value) <= np.float128(threshold): next_node = self._traverse_tree(sample, left_node) # left_node else: next_node = self._traverse_tree(sample, right_node) # right_node return next_node def predict(self, samples: pd.DataFrame): # apply traverse_tree method for each row in a dataframe results = samples.apply(self._traverse_tree, args=(self.tree,), axis=1) return np.array(results.astype(self._y_dtype))Код для отрисовки графиков
def tree_plot(sklearn_tree, Xa_train): plt.figure(figsize=(12, 18)) # customize according to the size of your tree plot_tree(sklearn_tree, feature_names=Xa_train.columns, filled=True, precision=6) plt.show() def tree_scores_plot(estimator, ccp_alphas, train_data, test_data, metric, labels): train_scores, test_scores = [], [] X_train, y_train = train_data X_test, y_test = test_data x_label, y_label = labels for ccp_alpha_i in ccp_alphas: estimator.ccp_alpha = ccp_alpha_i estimator.fit(X_train, y_train) train_pred_res = estimator.predict(X_train) test_pred_res = estimator.predict(X_test) train_score = metric(train_pred_res, y_train) test_score = metric(test_pred_res, y_test) train_scores.append(train_score) test_scores.append(test_score) fig, ax = plt.subplots() ax.set_xlabel(x_label) ax.set_ylabel(y_label) ax.set_title(f"{y_label} vs {x_label} for training and testing sets") ax.plot(ccp_alphas, train_scores, marker="o", label="train", drawstyle="steps-post") ax.plot(ccp_alphas, test_scores, marker="o", label="test", drawstyle="steps-post") ax.legend() plt.show() def decision_boundary_plot(X, y, X_train, y_train, clf, feature_indexes, title=None): if y.dtype != 'int': y = pd.Series(LabelEncoder().fit_transform(y)) y_train = pd.Series(LabelEncoder().fit_transform(y_train)) feature1_name, feature2_name = X.columns[feature_indexes] X_feature_columns = X.values[:, feature_indexes] X_train_feature_columns = X_train.values[:, feature_indexes] clf.fit(X_train_feature_columns, y_train.values) plot_decision_regions(X=X_feature_columns, y=y.values, clf=clf) plt.xlabel(feature1_name) plt.ylabel(feature2_name) plt.title(title)Загрузка датасетов
Для обучения моделей будет использован Iris dataset, где необходимо верно определить типы цветков на основе их признаков. В случае регрессии используется load_linnerud dataset из scikit-learn.
df_path = "/content/drive/MyDrive/iris.csv" iris = pd.read_csv(df_path) X1, y1 = iris.iloc[:, :-1], iris.iloc[:, -1] X1_train, X1_test, y1_train, y1_test = train_test_split(X1, y1, test_size=0.3, random_state=0) print(iris) sepal_length sepal_width petal_length petal_width species 0 5.1 3.5 1.4 0.2 setosa 1 4.9 3.0 1.4 0.2 setosa 2 4.7 3.2 1.3 0.2 setosa 3 4.6 3.1 1.5 0.2 setosa 4 5.0 3.6 1.4 0.2 setosa .. ... ... ... ... ... 145 6.7 3.0 5.2 2.3 virginica 146 6.3 2.5 5.0 1.9 virginica 147 6.5 3.0 5.2 2.0 virginica 148 6.2 3.4 5.4 2.3 virginica 149 5.9 3.0 5.1 1.8 virginica [150 rows x 5 columns]X2, y2 = load_linnerud(return_X_y=True, as_frame=True) y2 = y2['Pulse'] X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y2, test_size=0.2, random_state=0) print(X2, y2, sep='n') Chins Situps Jumps 0 5.0 162.0 60.0 1 2.0 110.0 60.0 2 12.0 101.0 101.0 3 12.0 105.0 37.0 4 13.0 155.0 58.0 5 4.0 101.0 42.0 6 8.0 101.0 38.0 7 6.0 125.0 40.0 8 15.0 200.0 40.0 9 17.0 251.0 250.0 10 17.0 120.0 38.0 11 13.0 210.0 115.0 12 14.0 215.0 105.0 13 1.0 50.0 50.0 14 6.0 70.0 31.0 15 12.0 210.0 120.0 16 4.0 60.0 25.0 17 11.0 230.0 80.0 18 15.0 225.0 73.0 19 2.0 110.0 43.0 0 50.0 1 52.0 2 58.0 3 62.0 4 46.0 5 56.0 6 56.0 7 60.0 8 74.0 9 56.0 10 50.0 11 52.0 12 64.0 13 50.0 14 46.0 15 62.0 16 54.0 17 52.0 18 54.0 19 68.0 Name: Pulse, dtype: float64Обучение моделей и оценка полученных результатов
В случае классификации дерево на данных ирис показало высокую точность. После прунинга точность не увеличилась, зато удалось найти более оптимальное дерево (alpha=0.0143) с такой же точностью и меньшим количеством узлов.
А вот в случае регрессии удалось получить прирост в плане точности, подобрав alpha=3.613, которое создаёт дерево с минимальной ошибкой на тестовом наборе. Все результаты приведены ниже.
Для более удобного отображения полученных результатов в ручных реализациях лучше использовать скачанный ноутбук в самом начале.
Классификация до прунинга
tree_classifier = DecisionTreeCART() tree_classifier.fit(X1_train, y1_train) clf_ccp_alphas, _ = tree_classifier.cost_complexity_pruning_path(X1_train, y1_train) clf_ccp_alphas = clf_ccp_alphas[:-1] sk_tree_classifier = DecisionTreeClassifier(random_state=0) sk_tree_classifier.fit(X1_train, y1_train) sk_clf_path = sk_tree_classifier.cost_complexity_pruning_path(X1_train, y1_train) sk_clf_ccp_alphas = sk_clf_path.ccp_alphas[:-1] sk_clf_estimator = DecisionTreeClassifier(random_state=0) train1_data, test1_data = [X1_train, y1_train], [X1_test, y1_test] metric = accuracy_score labels = ['Alpha', 'Accuracy'] pprint(tree_classifier.tree, width=180) tree_plot(sk_tree_classifier, X1_train) print(f'tree alphas: {clf_ccp_alphas}', f'sklearn alphas: {sk_clf_ccp_alphas}', sep='n') tree_scores_plot(sk_clf_estimator, clf_ccp_alphas, train1_data, test1_data, metric, labels) {'petal_width <= 0.75 | as_leaf virginica error_rate 0.6643083900226757': ['setosa | error_rate 0.0', {'petal_length <= 4.95 | as_leaf virginica error_rate 0.33480885311871234': [{'petal_width <= 1.65 | as_leaf versicolor error_rate 0.0521008403361345': ['versicolor ' '| ' 'error_rate ' '0.0', {'sepal_width <= 3.1 | as_leaf virginica error_rate 0.014285714285714287': ['virginica ' '| ' 'error_rate ' '0.0', 'versicolor ' '| ' 'error_rate ' '0.0']}]}, {'petal_width <= 1.75 | as_leaf virginica error_rate 0.018532818532818515': [{'petal_width <= 1.65 | as_leaf virginica error_rate 0.014285714285714287': ['virginica ' '| ' 'error_rate ' '0.0', 'versicolor ' '| ' 'error_rate ' '0.0']}, 'virginica ' '| ' 'error_rate ' '0.0']}]}]} 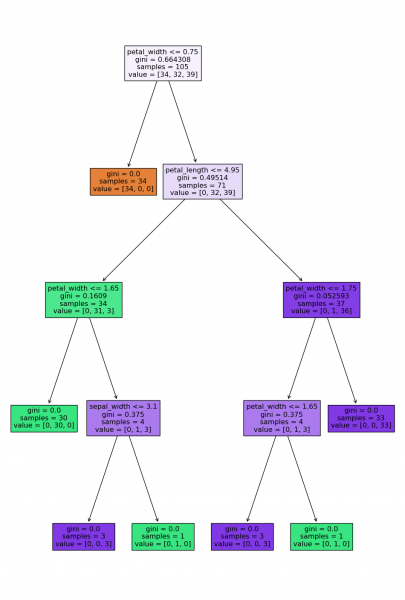
tree alphas: [0. 0.00926641 0.01428571 0.03781513 0.26417519] sklearn alphas: [0. 0.00926641 0.01428571 0.03781513 0.26417519]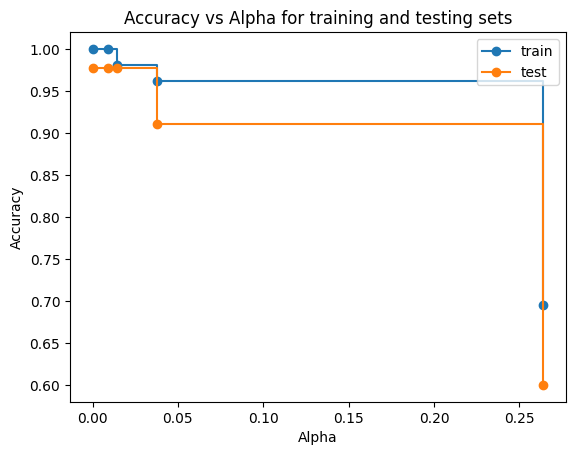
Классификация после прунинга
tree_clf_prediction = tree_classifier.predict(X1_test) tree_clf_accuracy = accuracy_score(tree_clf_prediction, y1_test) sk_tree_clf_prediction = sk_tree_classifier.predict(X1_test) sk_clf_accuracy = accuracy_score(sk_tree_clf_prediction, y1_test) best_clf_ccp_alpha = 0.0143 # based on a plot best_tree_classifier = DecisionTreeCART(ccp_alpha=best_clf_ccp_alpha) best_tree_classifier.fit(X1_train, y1_train) best_tree_clf_prediction = best_tree_classifier.predict(X1_test) best_tree_clf_accuracy = accuracy_score(best_tree_clf_prediction, y1_test) best_sk_tree_classifier = DecisionTreeClassifier(random_state=0, ccp_alpha=best_clf_ccp_alpha) best_sk_tree_classifier.fit(X1_train, y1_train) best_sk_tree_clf_prediction = best_sk_tree_classifier.predict(X1_test) best_sk_clf_accuracy = accuracy_score(best_sk_tree_clf_prediction, y1_test) print('tree prediction', tree_clf_prediction, ' ', sep='n') print('sklearn prediction', sk_tree_clf_prediction, ' ', sep='n') print('best tree prediction', best_tree_clf_prediction, ' ', sep='n') print('best sklearn prediction', best_sk_tree_clf_prediction, ' ', sep='n') pprint(best_tree_classifier.tree, width=180) tree_plot(best_sk_tree_classifier, X1_train) print(f'our tree pruning accuracy: before {tree_clf_accuracy} -> after {best_tree_clf_accuracy}') print(f'sklearn tree pruning accuracy: before {sk_clf_accuracy} -> after {best_sk_clf_accuracy}') tree prediction ['virginica' 'versicolor' 'setosa' 'virginica' 'setosa' 'virginica' 'setosa' 'versicolor' 'versicolor' 'versicolor' 'virginica' 'versicolor' 'versicolor' 'versicolor' 'versicolor' 'setosa' 'versicolor' 'versicolor' 'setosa' 'setosa' 'virginica' 'versicolor' 'setosa' 'setosa' 'virginica' 'setosa' 'setosa' 'versicolor' 'versicolor' 'setosa' 'virginica' 'versicolor' 'setosa' 'virginica' 'virginica' 'versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor' 'virginica' 'setosa' 'virginica' 'setosa' 'setosa'] sklearn prediction ['virginica' 'versicolor' 'setosa' 'virginica' 'setosa' 'virginica' 'setosa' 'versicolor' 'versicolor' 'versicolor' 'virginica' 'versicolor' 'versicolor' 'versicolor' 'versicolor' 'setosa' 'versicolor' 'versicolor' 'setosa' 'setosa' 'virginica' 'versicolor' 'setosa' 'setosa' 'virginica' 'setosa' 'setosa' 'versicolor' 'versicolor' 'setosa' 'virginica' 'versicolor' 'setosa' 'virginica' 'virginica' 'versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor' 'virginica' 'setosa' 'virginica' 'setosa' 'setosa'] best tree prediction ['virginica' 'versicolor' 'setosa' 'virginica' 'setosa' 'virginica' 'setosa' 'versicolor' 'versicolor' 'versicolor' 'virginica' 'versicolor' 'versicolor' 'versicolor' 'versicolor' 'setosa' 'versicolor' 'versicolor' 'setosa' 'setosa' 'virginica' 'versicolor' 'setosa' 'setosa' 'virginica' 'setosa' 'setosa' 'versicolor' 'versicolor' 'setosa' 'virginica' 'versicolor' 'setosa' 'virginica' 'virginica' 'versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor' 'virginica' 'setosa' 'virginica' 'setosa' 'setosa'] best sklearn prediction ['virginica' 'versicolor' 'setosa' 'virginica' 'setosa' 'virginica' 'setosa' 'versicolor' 'versicolor' 'versicolor' 'virginica' 'versicolor' 'versicolor' 'versicolor' 'versicolor' 'setosa' 'versicolor' 'versicolor' 'setosa' 'setosa' 'virginica' 'versicolor' 'setosa' 'setosa' 'virginica' 'setosa' 'setosa' 'versicolor' 'versicolor' 'setosa' 'virginica' 'versicolor' 'setosa' 'virginica' 'virginica' 'versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor' 'virginica' 'setosa' 'virginica' 'setosa' 'setosa'] {'petal_width <= 0.75 | as_leaf virginica error_rate 0.6643083900226757': ['setosa | error_rate 0.0', {'petal_length <= 4.95 | as_leaf virginica error_rate 0.33480885311871234': [{'petal_width <= 1.65 | as_leaf versicolor error_rate 0.0521008403361345': ['versicolor ' '| ' 'error_rate ' '0.0', 'virginica ' 'error_rate ' '0.014285714285714287']}, 'virginica error_rate ' '0.018532818532818515']}]}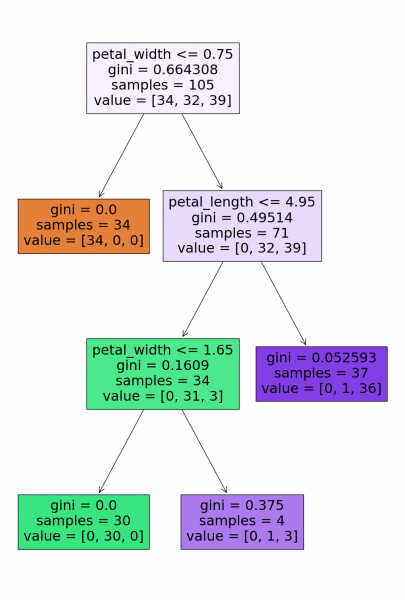
our tree pruning accuracy: before 0.9777777777777777 -> after 0.9777777777777777 sklearn tree pruning accuracy: before 0.9777777777777777 -> after 0.9777777777777777Визуализация решающих границ до и после прунинга
feature_indexes = [2, 3] title1 = 'Classification tree surface before pruning' decision_boundary_plot(X1, y1, X1_train, y1_train, sk_tree_classifier, feature_indexes, title1)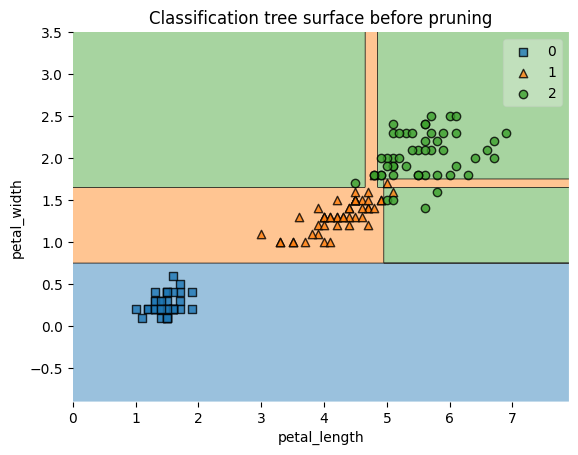
feature_indexes = [2, 3] title2 = 'Classification tree surface after pruning' decision_boundary_plot(X1, y1, X1_train, y1_train, best_sk_tree_classifier, feature_indexes, title2)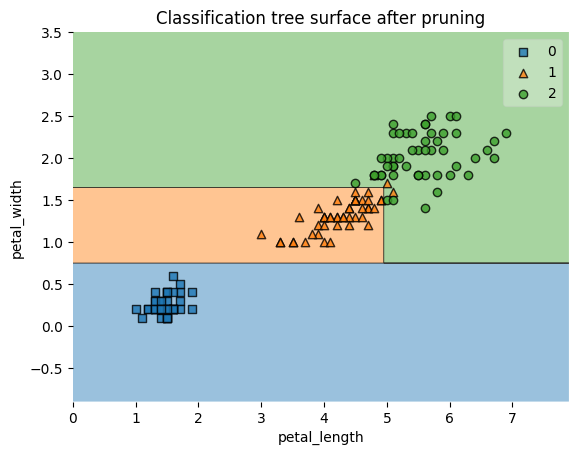
feature_indexes = [2, 3] plt.figure(figsize=(10, 15)) for i, alpha in enumerate(clf_ccp_alphas): sk_tree_clf = DecisionTreeClassifier(random_state=0, ccp_alpha=alpha) plt.subplot(3, 2, i + 1) plt.subplots_adjust(hspace=0.5) title = f'ccp_alpha = {alpha}' decision_boundary_plot(X1, y1, X1_train, y1_train, sk_tree_clf, feature_indexes, title)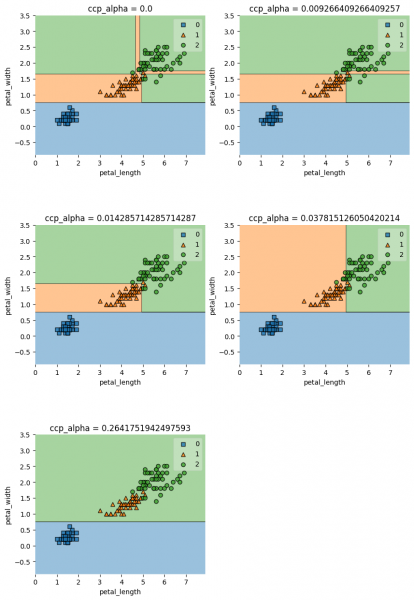
Прунинг при всех полученных alpha ccp
Регрессия до прунинга
tree_regressor = DecisionTreeCART(regression=True) tree_regressor.fit(X2_train, y2_train) reg_ccp_alphas, _ = tree_regressor.cost_complexity_pruning_path(X2_train, y2_train) reg_ccp_alphas = reg_ccp_alphas[:-1] sk_tree_regressor = DecisionTreeRegressor(random_state=0) sk_tree_regressor.fit(X2_train, y2_train) sk_reg_path = sk_tree_regressor.cost_complexity_pruning_path(X2_train, y2_train) sk_reg_ccp_alphas = sk_reg_path.ccp_alphas[:-1] reg_estimator = DecisionTreeCART(regression=True) sk_reg_estimator = DecisionTreeRegressor(random_state=0) train2_data, test2_data = [X2_train, y2_train], [X2_test, y2_test] metric = mean_absolute_percentage_error labels = ['Alpha', 'MAPE'] pprint(tree_regressor.tree) tree_plot(sk_tree_regressor, X2_train) print(f'CART alphas: {reg_ccp_alphas}') tree_scores_plot(reg_estimator, reg_ccp_alphas, train2_data, test2_data, metric, labels) print(f'sklearn_alphas: {sk_reg_ccp_alphas}') tree_scores_plot(sk_reg_estimator, sk_reg_ccp_alphas, train2_data, test2_data, metric, labels) {'Jumps <= 90.5 | as_leaf 54.625 error_rate 29.359375': [{'Jumps <= 46.0 | as_leaf 52.90909090909091 error_rate 17.181818181818183': [{'Jumps <= 34.0 | as_leaf 54.857142857142854 error_rate 11.428571428571429': [{'Jumps <= 28.0 | as_leaf 50.0 error_rate 2.0': ['54.0 ' '| ' 'error_rate ' '0.0', '46.0 ' '| ' 'error_rate ' '0.0']}, {'Chins <= 14.5 | as_leaf 56.8 error_rate 5.3': [{'Situps <= 103.0 | as_leaf 58.5 error_rate 1.6875': ['56.0 ' '| ' 'error_rate ' '0.0', {'Jumps <= 38.5 | as_leaf 61.0 error_rate 0.125': ['62.0 ' '| ' 'error_rate ' '0.0', '60.0 ' '| ' 'error_rate ' '0.0']}]}, '50.0 ' '| ' 'error_rate ' '0.0']}]}, {'Chins <= 12.0 | as_leaf 49.5 error_rate 1.1875': [{'Jumps <= 70.0 | as_leaf 50.666666666666664 error_rate 0.16666666666666666': ['50.0 ' '| ' 'error_rate ' '0.0', '52.0 ' '| ' 'error_rate ' '0.0']}, '46.0 ' '| ' 'error_rate ' '0.0']}]}, {'Jumps <= 110.0 | as_leaf 58.4 error_rate 5.7': [{'Jumps <= 103.0 | as_leaf 61.0 error_rate 1.125': ['58.0 ' '| ' 'error_rate ' '0.0', '64.0 ' '| ' 'error_rate ' '0.0']}, {'Chins <= 12.5 | as_leaf 56.666666666666664 error_rate 3.1666666666666665': ['62.0 ' '| ' 'error_rate ' '0.0', {'Jumps <= 182.5 | as_leaf 54.0 error_rate 0.5': ['52.0 ' '| ' 'error_rate ' '0.0', '56.0 ' '| ' 'error_rate ' '0.0']}]}]}]}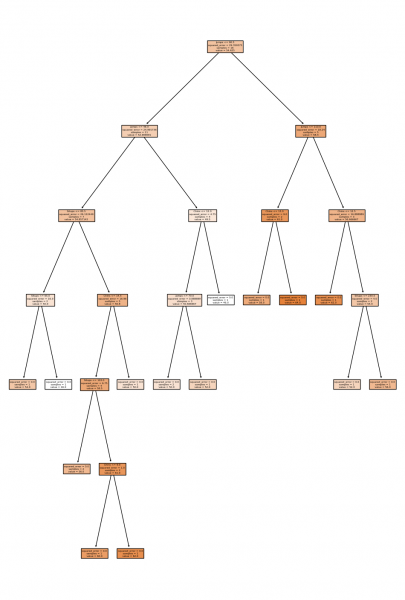
CART alphas: [0. 0.125 0.16666667 0.5 1.02083333 1.125 1.5625 2. 2.0375 3.6125 4.12857143 4.56574675]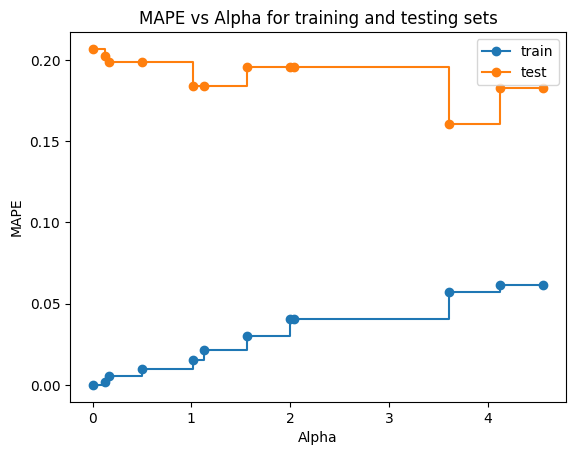
sklearn_alphas: [0. 0.125 0.16666667 0.5 1.02083333 1.125 1.5625 2. 2.0375 3.6125 4.12857143 4.56574675]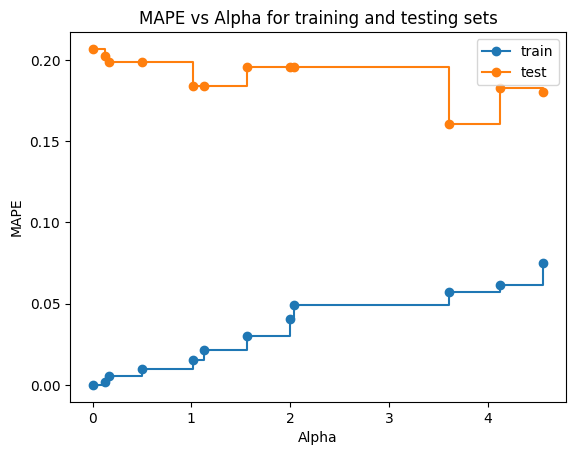
Регрессия после прунинга
tree_reg_prediction = tree_regressor.predict(X2_test) tree_reg_error = mean_absolute_percentage_error(tree_reg_prediction, y2_test) sk_tree_reg_prediction = sk_tree_regressor.predict(X2_test) sk_reg_error= mean_absolute_percentage_error(sk_tree_reg_prediction, y2_test) best_reg_ccp_alpha = 3.613 # based on a plot best_tree_regressor = DecisionTreeCART(ccp_alpha=best_reg_ccp_alpha, regression=True) best_tree_regressor.fit(X2_train, y2_train) best_tree_reg_prediction = best_tree_regressor.predict(X2_test) lowest_tree_reg_error = mean_absolute_percentage_error(best_tree_reg_prediction, y2_test) best_sk_tree_regressor = DecisionTreeRegressor(random_state=0, ccp_alpha=best_reg_ccp_alpha) best_sk_tree_regressor.fit(X2_train, y2_train) best_sk_tree_reg_prediction = best_sk_tree_regressor.predict(X2_test) lowest_sk_reg_error = mean_absolute_percentage_error(best_sk_tree_reg_prediction, y2_test) print('tree prediction', tree_reg_prediction, ' ', sep='n') print('sklearn prediction', sk_tree_reg_prediction, ' ', sep='n') print('best tree prediction', best_tree_reg_prediction, ' ', sep='n') print('best sklearn prediction', best_sk_tree_reg_prediction, ' ', sep='n') pprint(best_tree_regressor.tree) tree_plot(best_sk_tree_regressor, X2_train) print(f'tree error: before {tree_reg_error} -> after pruning {lowest_tree_reg_error}') print(f'sklearn tree error: before {sk_reg_error} -> after pruning {lowest_sk_reg_error}') tree prediction [46. 50. 60. 50.] sklearn prediction [46. 50. 60. 50.] best tree prediction [49.5 49.5 56.8 56.8] best sklearn prediction [49.5 49.5 56.8 56.8] {'Jumps <= 90.5 | as_leaf 54.625 error_rate 29.359375': [{'Jumps <= 46.0 | as_leaf 52.90909090909091 error_rate 17.181818181818183': [{'Jumps <= 34.0 | as_leaf 54.857142857142854 error_rate 11.428571428571429': ['50.0 ' 'error_rate ' '2.0', '56.8 ' 'error_rate ' '5.3']}, '49.5 ' 'error_rate ' '1.1875']}, '58.4 error_rate 5.7']}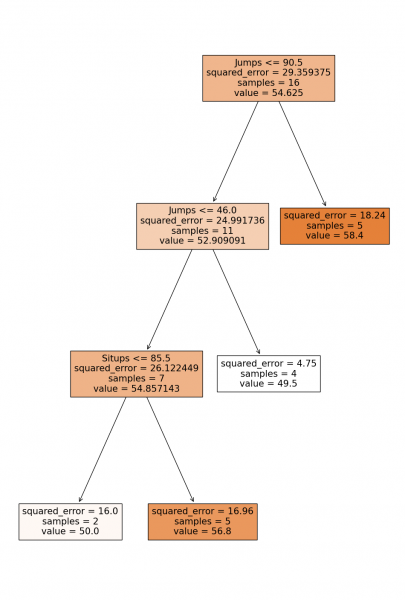
tree error: before 0.20681159420289855 -> after pruning 0.16035353535353536 sklearn tree error: before 0.20681159420289855 -> after pruning 0.1603535353535354Преимущества и недостатки дерева решений
Преимущества:
-
простота в интерпретации и визуализации;
-
неплохая работа с нелинейными зависимостями в данных;
-
не требуется особой подготовки тренировочного набора;
-
относительно высокая скорость обучения и прогнозирования.
Недостатки:
-
поиск оптимального дерева является NP-полной задачей;
-
нестабильность работы даже при небольшом изменении данных;
-
возможность переобучения из-за чувствительности к шуму и выбросам в данных.
Дополнительные источники
Статья «The CART Decision Tree for Mining Data Streams», Leszek Rutkowskia, Maciej Jaworskia, Lena Pietruczuka, Piotr Dudaa.
Документация:
-
описание CART ;
-
DecisionTreeClassifier ;
-
DecisionTreeRegressor ;
-
pruning .
Лекции: один, два, три, четыре.
Пошаговое построение дерева решений: один, два, три.
Pruning:
-
Статья.
-
Видео: один, два, три.
Бэггинг и случайный лес 🡆
